تشابه المثلثات
صفحة 1 من اصل 1
تشابه المثلثات
من طرف refathafez الجمعة 19 ديسمبر 2014, 11:11 pm
المتطلبات المسبقة : من الضروري أن يعرف الدارس طريقة رسم المثلث إذا عرف :
1) أطوال أضلاعه الثلاثة .
2) طولا ضلعين والزاوية المحصورة بينهما .
3) طول كل من ضلعي القائمة في مثلث قائم الزاوية .
4) قيم زاويتين من زواياه وطول أحد أضلاعه .
الأهداف : يتوقع من الدارس بعد نهاية دراسة الموضوع أن :
1- يستنتج الشروط الواجب توافرها لتشابه مثلثين .
2- يطبق علاقة تشابه المثلثين في مواقف جديدة .
1- ارسم مثلثاً متساوي الأضلاع ، كم مقدار كل زاوية من زواياه ؟
2- لماذا لا يمكنك رسم مثلث فيه زاويتان قائمتان ؟
3- أكمل العبارة : يجب أن يكون في أي مثلث زاويتان .............. على الأقل أما الزاوية الثالثة فيمكن أن تكون .............. أو .............. أو ................ .
4- أجب عن الأسئلة التالية بالترتيب :
أ) إذا كان طول القطعة المستقيمة س ص = 6سم ، وطول القطعة المستقيمة ع ل = 10سم ،
فما نسبة طول س ص إلى ع ل ؟
ب) إذا كان طول القطعة المستقيمة م ط = 15سم وطول القطعة المستقيمة ق ك = 25سم ،
فما نسبة طول م ط إلى ق ك ؟
(من الفرع ب) |  | (من الفرع أ) = |  | ج) أثبت أن |
| = | | د) ماذا نسمي العلاقة السابقة |
وكان ح ي = 30سم ، رف = 20سم ، وكان ش ت = 36 سم . |  | = |  | ﻫ) إذا كان |
فما طول ض و ؟
إجابات الأسئلة :
1- ارسم مثلثاً متساوي الأضلاع ، كم مقدار كل زاوية من زواياه ؟
كل زاوية من زوايا المثلث المتساوي الأضلاع = 60 ْ.
كل زاوية من زوايا المثلث المتساوي الأضلاع = 60 ْ.
2- لماذا لا يمكنك رسم مثلث فيه زاويتان قائمتان ؟
لأن مجموع زوايا المثلث = 180 ْ فتكون الزاوية الثالثة = صفر إذن لا يمكن رسم مثلث في هذه الحالة إذ لا توجد زاوية ثالثة .
3- أكمل العبارة :
يجب أن يكون في أي مثلث زاويتان { حادتان } على الأقل أما الزاوية الثالثة فيمكن أن تكون {حادة} أو { قائمة }
أو { منفرجة } .
يجب أن يكون في أي مثلث زاويتان { حادتان } على الأقل أما الزاوية الثالثة فيمكن أن تكون {حادة} أو { قائمة }
أو { منفرجة } .
4- أ ) إذا كان طول القطعة المستقيمة س ص = 6سم ، وطول القطعة المستقيمة ع ل = 10 سم ، فما نسبة طول س ص إلى ع ل ؟
| بالاختصار إلى أبسط صورة . | 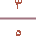 | = |  | = | | الجواب : |
4 - ب ) إذا كان طول القطعة المستقيمة م ط = 15سم وطول القطعة المستقيمة ق ك = 25 سم ،فما نسبة طول م ط إلى ق ك؟
| كالسابق . | 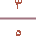| = |  | = | تشابه المثلثات اختبار التعلم القبلي :
الجواب : نسميها تناسباً والتناسب هو تساوي نسبتين أو أكثر. مثل :
30 × ض و = 20 × 36 ( بقسمة الطرفين على 30 ثم الاختصار ) ض و = 24 سم.ارتفاع المثلث أ ب ج = 5.2 سم تقريباً و ارتفاع المثلث ك م ن = 3.4 سم تقريباً . نسبة أ ب : ك م هي 3 : 2 وكذلك نسبة أ د : ك هـ هي 3 : 2 ( تقريباً )
| الجواب | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ـ ارسم مثلثاً متساوي الأضلاع ( على دفترك ) طول ضلعه 3 سم وسمه ق ر غ . أنزل عموداً ق و على ر غ ، قس طول العمود وسجله على دفترك .
[rtl]ـ أكمل العبارات التالية التي تربط بين المثلثين أ ب جـ ، ق رغ .[/rtl]
[rtl]  [/rtl] |
[rtl]  [/rtl] |
[rtl]  [/rtl] |
[rtl]4. أكمل الفراغ في العبارة :[/rtl] |
[rtl]  [/rtl] |
[rtl]  [/rtl] |
[rtl]6. المثلثان أ ب جـ ، ق رغ هما من النوع المتساوي الأضلاع وزواياهما متساوية وقيمة كل زاوية منها =[/rtl]
[rtl] .............. درجة.[/rtl]
[rtl]7. إذا ساوت كل زاوية في مثلث ما نظيرتها في مثلث آخر ( مثلثان متساويان في الزوايا ) فنطلق عليهما اسم[/rtl]
[rtl] " مثلثان متشابهان " وعلى ذلك فإن المثلث أ ب ج يشبه المثلث ك م ن يشبه المثلث ......... .[/rtl]
[rtl]8. كل المثلثات المتساوية الأضلاع ....... لأنها جميعاً متساوية في زواياها .[/rtl]
[rtl]الإجابات[/rtl]
[rtl]لإجابات :[/rtl]
[rtl]الجواب :  [/rtl] | |
[rtl]الجواب :  [/rtl] | |
[rtl]الجواب :  [/rtl] | |
[rtl]4. أكمل الفراغ في العبارة :[/rtl] | |
 | |
 | [rtl]5.[/rtl] |
[rtl]6. المثلثان أ ب جـ ، ق رغ هما من النوع المتساوي الأضلاع وزواياهما متساوية وقيمة كل زاوية منها =60 درجة.[/rtl]
[rtl]7. إذا ساوت كل زاوية في مثلث ما نظيرتها في مثلث آخر ( مثلثان متساويان في الزوايا ) فنطلق عليهما اسم " مثلثان متشابهان " وعلى ذلك فإن المثلث أ ب ج يشبه المثلث ك م ن يشبه المثلث ق ر ع .[/rtl]
[rtl]8. كل المثلثات المتساوية الأضلاع متشابهة لأنها جميعاً متساوية في زواياها .[/rtl]
سؤال (1) :
ط ع ل مثلث متساوي الأضلاع وطول ضلعه 8سم . ط ص هو ارتفاع لهذا المثلث .
ك م ن مثلثٌ آخر متساوي الأضلاع وطول ضلعه 4سم . أُنْزِل العمود ك هـ من النقطة ك على الضلع م ن .
*ارسم كل حالة من الحالتين . وقس طول ط ص ، ك هـ .
* حدِّد الإشارة الصحيحة في الفراغات التالية :(= ، > ، <)
* حدِّد الإشارة الصحيحة في الفراغات التالية :(= ، > ، <)
* هل المثلثان متشابهان ؟ فسر جوابك ؟
ط ع ........ ط ص
ط ص ........ ك هـ
 | ........... |  |
refathafez- المدير
-
عدد الرسائل : 698
العمر : 61
تاريخ التسجيل : 26/10/2008 -
رد: تشابه المثلثات
من طرف refathafez الجمعة 19 ديسمبر 2014, 11:15 pm
تدريب تقويمي :
تدريب (3) :
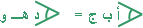| . |  | وكذلك | 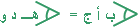 | في المثلثين أ ب ج ، د هـ و ، |
المطلوب : أ) أثبت أن المثلثين متشابهان ؟ | ||||
ب) كم مثلثاً متشابهاً يمكنك أن ترسم حسب الشروط المعطاة في نص السؤال . فسِّر إجابتك .
تدريب (4) :
 | في المثلثين س ص ك ، هـ م ل |
المطلوب : أ) إثبات أنهما متشابهان .
ب) كم مثلثاً يمكنك رسمه حسب الشروط المعطاة ؟ فسِّر إجابتك .
ب) كم مثلثاً يمكنك رسمه حسب الشروط المعطاة ؟ فسِّر إجابتك .
إجابة تدريب (3) :
البرهان :
البرهان :
\ المثلثان متشابهان لتساوي زواياهما كل واحدة مع الأخرى .
عدد المثلثات التي يمكن رسمها لا حصر لها ، حتى لو كانت قيمة كل زاوية معروفة فإن أطوال الأضلاع التي يمكن رسم المثلثات بها تبقى غير محدودة . باختصار عدد المثلثات له قيمة مطلقة .
إجابة تدريب (4):
البرهان :
أ) ما دامت النسبة بين أطوال أضلاع المثلثين كل لنظيره ( 3 : 4 ) ثابتة إذن المثلثان متشابهان .
ب) عدد المثلثات له قيمة مطلقة (لماذا ؟)
أ) ما دامت النسبة بين أطوال أضلاع المثلثين كل لنظيره ( 3 : 4 ) ثابتة إذن المثلثان متشابهان .
ب) عدد المثلثات له قيمة مطلقة (لماذا ؟)
refathafez- المدير
-
عدد الرسائل : 698
العمر : 61
تاريخ التسجيل : 26/10/2008 -
رد: تشابه المثلثات
من طرف refathafez الجمعة 19 ديسمبر 2014, 11:18 pm
خلاصة :
أكمل العبارات التالية بوضع كلمة واحدة في الفراغ الواحد .
أ) يكون المثلثان متشابهين إذا كانت زوايا المثلث الأول تساوي ــــــ المثلث الثاني .
 | ب) في المثلثين س ك د ، ص هـ م ، |
| إذن المثلثان س ك د ، ص هـ م ـــــــ . | |
إذن المثلثان ـــــــ . |  | ج) في المثلثين ج ص ل ، ح ط ي : |
 | ولكنها لا تساوي |  | د) في المثلثين ع م ق ، ص ط ل النسبة | |
إذن المثلثان غير ــــــ . |
ﻫ) إذا تساوت زوايا مثلثين كانت النسبة بين أضلاعهما كل لنظيره = مقداراً ـــــ وكان المثلثان متشابهين .
و) إذا تساوت النسب بين أطوال أضلاع مثلثين كل لنظيره ، كانت كل زاوية في المثلث الأول = نظيرتها في المثلث الثاني وكان المثلثان ــــــ .
الخلاصة :
أكمل العبارات التالية بوضع كلمة واحدة في الفراغ الواحد .
أ) يكون المثلثان متشابهين إذا كانت زوايا المثلث الأول تساوي زوايا المثلث الثاني .
| ب) في المثلثين س ك د ، ص هـ م ، |
إذن المثلثان س ك د ، ص هـ م متشابهان . | |
إذن المثلثان متشابهان . | | ج) في المثلثين ج ص ل ، ح ط ي : |
| ولكنها لا تساوي | | د) في المثلثين ع م ق ، ص ط ل النسبة | |
إذن المثلثان غير متشابهين . |
هـ) إذا تساوت زوايا مثلثين كانت النسبة بين أضلاعهما كل لنظيره = مقداراً ثابتاً وكان المثلثان متشابهين .
و) إذا تساوت النسب بين أطوال أضلاع مثلثين كل لنظيره ، كانت كل زاوية في المثلث الأول = نظيرتها في المثلث الثاني وكان المثلثان متشابهين .
refathafez- المدير
-
عدد الرسائل : 698
العمر : 61
تاريخ التسجيل : 26/10/2008 -
رد: تشابه المثلثات
من طرف refathafez الجمعة 19 ديسمبر 2014, 11:20 pm
سؤال (4) :
ارسم المثلث أ ب ج حيث أ ب =4سم ، ب ج = 5.5 سم ، أ ج = 2.5 سم .
ثم ارسم المثلث س ص ع حيث س ص = 6سم ، ص ع = 5سم ، س ع = 7سم .
1. ما أوجه الشبه بين المثلثين .
2. ما أوجه الاختلاف بينهما .
3. لماذا لا يمكن أن نسمي هذين المثلثين متشابهان ؟
1- لا يوجد أي وجه شبه فالأضلاع في كل منهما تختلف في طولها عن أطوال أضلاع الآخر ، وكذلك قيم الزوايا في كل منهما اتختلف عن قيمتها في الآخر .
2- أطوال الأضلاع مختلفة تماماً . قيم الزوايا مختلفة . المساحات مختلفة .
3- لعدم تساوي الزوايا في المثلثين كل مع نظيراتها ، لعدم وجود نسبة ثابتة بين أطوال الأضلاع .
فإذا أخذنا :
ج ب : ع س = 5.5 : 7 = 11 : 14 ( يقابلان أكبر زاويتين ) .
أ ب : س ص = 4 : 6 = 2 : 3 ( يقابلان الزاويتين الأقل قيمة من الزاوية الكبيرة في كل منهما) .
أ ج : ص ع = 2.5 : 5 = 2 : 1 ( يقابلان أصغر زاويتين ) .
2- أطوال الأضلاع مختلفة تماماً . قيم الزوايا مختلفة . المساحات مختلفة .
3- لعدم تساوي الزوايا في المثلثين كل مع نظيراتها ، لعدم وجود نسبة ثابتة بين أطوال الأضلاع .
فإذا أخذنا :
ج ب : ع س = 5.5 : 7 = 11 : 14 ( يقابلان أكبر زاويتين ) .
أ ب : س ص = 4 : 6 = 2 : 3 ( يقابلان الزاويتين الأقل قيمة من الزاوية الكبيرة في كل منهما) .
أ ج : ص ع = 2.5 : 5 = 2 : 1 ( يقابلان أصغر زاويتين ) .
refathafez- المدير
-
عدد الرسائل : 698
العمر : 61
تاريخ التسجيل : 26/10/2008 -
صفحة 1 من اصل 1
صلاحيات هذا المنتدى:
لاتستطيع الرد على المواضيع في هذا المنتدى